Como resolver a equação de uma linha reta através de dois pontos?

A matemática não é uma ciência chata, como parece às vezes. Há muitas coisas interessantes, embora às vezes incompreensíveis para aqueles que não querem entender. Hoje, será sobre um dos tópicos mais comuns e simples em matemática, ou melhor, a sua área que está à beira da álgebra e da geometria. Vamos falar sobre direto e suas equações. Parece que este é um assunto escolar chato, o que não promete nada interessante e novo. No entanto, isso não é assim, e neste artigo tentaremos provar a você o nosso ponto de vista. Antes de recorrer ao mais interessante e descrever a equação de uma linha direta através de dois pontos, recorremos à história de todas essas medidas, e depois descobrimos por que isso foi tudo necessário e por que agora também o conhecimento das fórmulas subseqüentes não interfere.

História

Mesmo nos tempos antigos, os matemáticos gostavam deconstruções geométricas e todos os tipos de gráficos. É difícil dizer hoje quem surgiu pela primeira vez com a equação de uma linha direta através de dois pontos. Mas podemos assumir que este homem era Euclid - um erudito e filósofo grego antigo. Foi ele quem, em seu tratado de "The Beginning", originou a base da futura geometria euclidiana. Agora, esta seção de matemática é considerada a base da representação geométrica do mundo e é ensinada na escola. Mas deve-se dizer que a geometria euclidiana opera apenas no nível macro em nossa medida tridimensional. Se considerarmos o cosmos, nem sempre é possível representar com ele todos os fenômenos que ocorrem lá.

Depois de Euclides, havia outros cientistas. E eles aperfeiçoaram e compreenderam o que ele descobriu e escreveu. No final, resultou uma área estável de geometria, na qual tudo ainda é inabalável. E, durante milênios, provou-se que a equação de uma linha direta em dois pontos é muito fácil de compilar. Mas antes de começar a explicar como fazer isso, vamos discutir um pouco de teoria.

Teoria

A linha é infinita nas duas direçõesUm segmento que pode ser dividido em um número infinito de segmentos de qualquer comprimento. Para representar uma linha reta, os gráficos são mais utilizados. E os gráficos podem ser tanto em um sistema de coordenadas tridimensional quanto em tridimensional. E eles são construídos de acordo com as coordenadas dos pontos que lhes pertencem. Afinal, se você olhar para uma linha reta, você pode ver que ela consiste em um conjunto infinito de pontos.

No entanto, há algo que a linha é muito fortedifere de outros tipos de linhas. Esta é a sua equação. Em geral, é muito simples, ao contrário, digamos, a equação de um círculo. Certamente, cada um de nós passou na escola. Mas ainda escreve sua forma geral: y = kx + b. Na próxima seção, vamos discutir em detalhes o que cada uma dessas letras significa e como resolver esta equação simples de uma linha direta que passa por dois pontos.

A equação da linha

A igualdade que foi apresentada acima, eé a equação necessária da linha. Vale a pena explicar o que aqui significa isso. Como você pode imaginar, y e x são as coordenadas de cada ponto que pertence a uma linha reta. Em geral, esta equação existe apenas porque, para cada ponto de qualquer linha, é peculiar estar em conexão com outros pontos e, portanto, existe uma lei que liga uma coordenada a outra. Esta lei determina como a equação de uma linha reta passa por dois pontos.

Por que dois pontos? Tudo isso ocorre porque o número mínimo de pontos necessários para construir uma linha reta no espaço bidimensional é de dois. Se tomarmos um espaço tridimensional, o número de pontos necessários para a construção de uma única linha reta também será igual a dois, já que três pontos já constituem um plano.

Há também um teorema que prova que é possível desenhar uma única linha reta através de dois pontos arbitrários. Este fato pode ser verificado na prática combinando dois pontos aleatórios no gráfico com uma régua.

Agora, considere um exemplo concreto e mostre como resolver esta equação notória de uma linha reta passando por dois pontos dados.

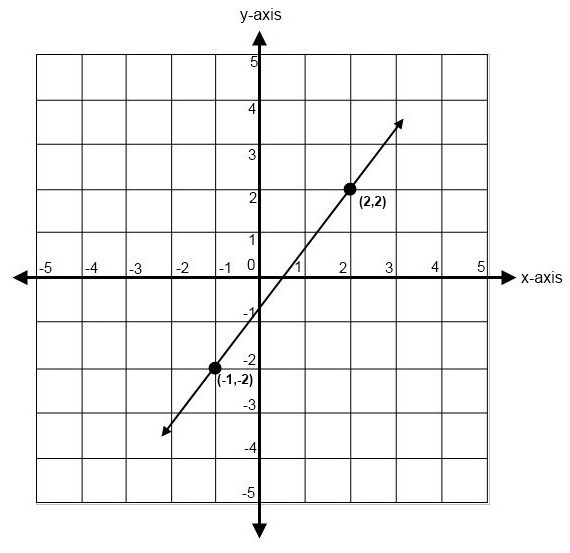
Exemplo:

Considere dois pontos através dos quais você deseja construir uma linha reta. Damos-lhes coordenadas, por exemplo, M₁(2; 1) e M₂(3; 2). Como sabemos do curso escolar, a primeira coordenada é o valor ao longo do eixo OX e a segunda é ao longo do eixo OY. A equação de uma linha reta através de dois pontos foi dada acima, e para descobrir os parâmetros faltantes k e b, precisamos compilar um sistema de duas equações. Na verdade, será composta por duas equações, cada uma das quais terá duas de nossas constantes desconhecidas:

1 = 2k + b

2 = 3k + b

Agora, o mais importante é o seguinte: para resolver este sistema. Isso é feito de forma bastante simples. Primeiro, expressamos a partir da primeira equação b: b = 1-2k. Agora precisamos substituir a equação resultante na segunda equação. Isso é feito substituindo b pela igualdade obtida por nós:

2 = 3k + 1-2k

1 = k;

Agora que sabemos qual é o valorcoeficiente k, é hora de descobrir o valor da constante seguinte - b. Isso é ainda mais fácil. Uma vez que conhecemos a dependência de b em k, podemos substituir o valor do último na primeira equação e descobrir o valor desconhecido:

b = 1-2 * 1 = -1.

Conhecendo os dois coeficientes, agora podemos substituí-losna equação geral inicial da linha reta através de dois pontos. Assim, para o nosso exemplo, obtemos a seguinte equação: y = x-1. Esta é a igualdade desejada que devemos ter obtido.

Antes de concluir, discutamos a aplicação desta seção de matemática no cotidiano.

Aplicação

Como tal, a equação de uma linha direta atravésDois pontos não são encontrados. Mas isso não significa que não precisamos disso. Na física e na matemática, as equações de linhas e propriedades, que se seguem, são muito usadas. Você pode nem perceber, mas a matemática nos rodeia. E até mesmo esses tópicos aparentemente não negociáveis ​​como a equação de uma linha direta através de dois pontos são muito úteis e muitas vezes aplicados em um nível fundamental. Se, à primeira vista, parece que isso não pode chegar a lugar algum, então você está enganado. A matemática desenvolve o pensamento lógico, que nunca será supérfluo.

Conclusão

Agora que descobrimos como criar linhas em dois pontos, não precisamos responder nenhuma dúvida relacionada a isso. Por exemplo, se um professor lhe disser: "Escreva a equação de uma linha reta passando por dois pontos, "então você não poderá fazer isso, esperamos que este artigo seja útil para você.